算法入门级介绍

A Breif Introduction of Algorithm

最近零散笔记写了不少，但还是应该系统成文，才能强化记忆。今天写一些基础却必须理解的算法知识。（本文偏概念不涉及代码，零基础阅读无压力）

算法的概念

算法是什么？

简言之，算法是独立存在的一种解决问题的方法和思想。

对于算法而言，重要是思想而非实现语言，所以同一种算法，可能有不同语言的实现版本（如：C描述、Java描述、Python描述等等）。

算法是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。即是说，能够对一定规范的输入，在有限时间内获得所要求的输出。

为了解决不同的具体问题会产生不同的算法，但空谈哪个算法更好是没有意义。

算法的5大特性

除了错误的算法，其它算法都应该符合算法的5大特性，具体如下：

输入(Input): 算法具有0个或多个输入。
输出(Output): 算法至少有1个或多个输出。
有穷性(Finiteness): 算法在有限的步骤之后会自动结束而不会无限循环，并且每一个步骤可以在可接受的时间内完成。
确定性(Definiteness)：算法中的每一步都有确定的含义，不会出现二义性。
可行性(Effectiveness)：算法的每一步都是可行的，也就是说每一步都能够执行有限的次数完成。

衡量算法效率

通常情况下，实现算法程序的执行时间可以反应出算法的效率，即算法的优劣。

衡量算法效率一般看这两个标准：时间效率和空间效率。

而在算法中与这两个标准直接相关的概念就是 时间复杂度 和 空间复杂度。

时间复杂度(Time Complexity)

算法时间复杂度是指执行算法所需要的计算工作量。算法的计算工作量用算法所执行的基本运算次数来度量。算法所执行的基本运算次数是问题规模的函数。

通常描述该算法的运行时间，通常用“大O表示法”表述。

大O表示法

对于算法的时间效率,可以用“大O表示法”，这是一种特殊的表示法，指出了算法的速度有多快。

时间复杂度：假设存在函数g，使得算法A处理规模为n的问题示例所用时间为T(n)=O(g(n))，则称O(g(n))为算法A的渐近时间复杂度，简称时间复杂度，记为T(n)

对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。

举个例子：可以认为3n^2和100n^2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n^2级。

最坏时间复杂度

分析算法时，存在几种可能的考虑：

算法完成工作最少需要多少基本操作，即最优时间复杂度
算法完成工作最多需要多少基本操作，即最坏时间复杂度
算法完成工作平均需要多少基本操作，即平均时间复杂度

对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

时间复杂度的计算规则

如果独立分析算法的时间复杂度呢，可以参考下面几条基本规则：

1.基本操作，即只有常数项，认为其时间复杂度为O(1)。
2.顺序结构，时间复杂度按加法进行计算。
3.循环结构，时间复杂度按乘法进行计算。
4.分支结构，时间复杂度取最大值。
5.判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略。
4.在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度。

常见时间复杂度及其关系

下面列出一些常见的时间复杂度。

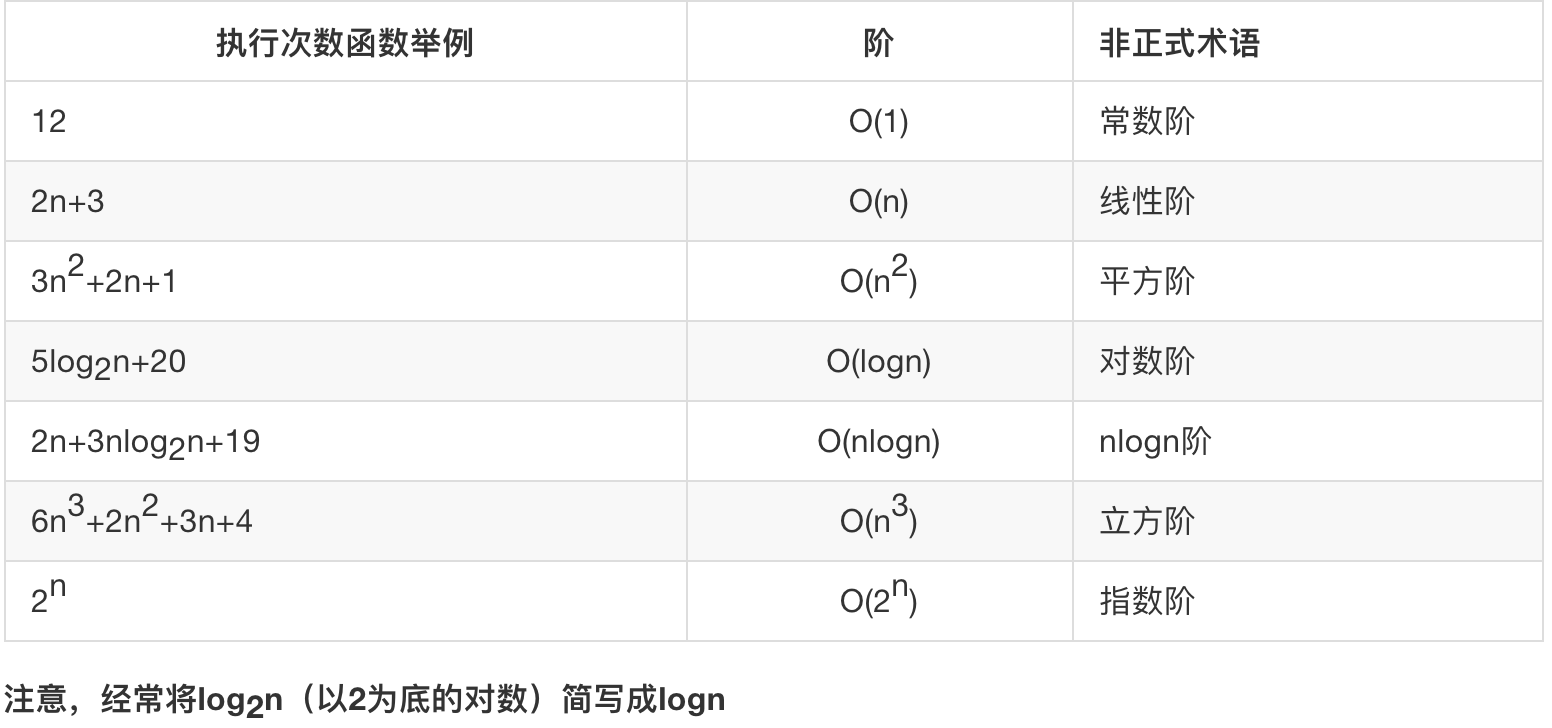
如果觉得不够直观可看下图：

由图可知，它们所消耗的时间从小到大为：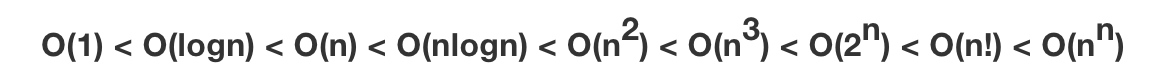

空间复杂度(Space Complexity)

算法的空间复杂度是指执行这个算法所需要的内存空间。一般记做S(n)=O(f(n))。

算法执行期间所需的存储空间包括3部分，空间复杂度包含的3部分分别是：输入数据所占的存储空间、程序本身所占的存储空间、算法执行过中所需要的额外空间。

评价算法效率的时候还是以时间复杂度作为主要指标的，就算谈论到空间复杂度也更倾向于第三个部分”算法执行过中所需要的额外空间”，特别是在OJ刷题的时候。

另外随着存储技术的进步，在空间换时间和时间换空间的选择上，只要在成本范围内，大家都更倾向于用空间换时间。因此，本文作为基础入门不再做深入探讨。